Intutions for Types of Sequence-to-Sequence Models#

RNN#

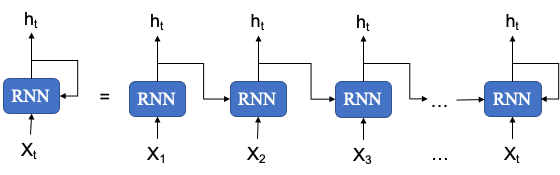
  • Vanishing gradient problems when modeling long-distance relationships

LSTM vs GRU#

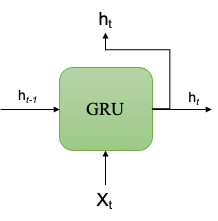
  • Possible solutions to the issues of vanishing gradients

  • Better modeling of long-term relationships

  • GRU is a simpler version of LSTM, rendering it easier to train computationally

Simple Sequence-to-Sequence Model#

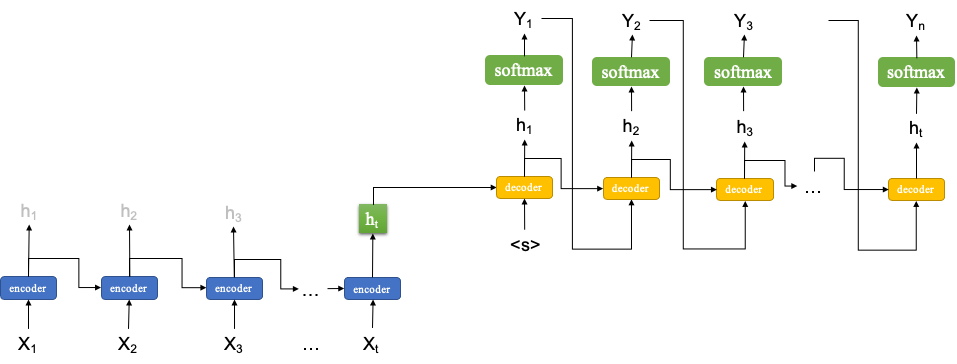
  • A schematic model representation of many-to-many sequence model

  • The input and output sizes can be different

  • A typical task is machine translation

  • Two sequence models need to be trained: encoder and decoder

  • Encoder:

    • A vanilla version of the seq-to-seq model takes the last return state \(h_t\) of the encoder as the initial and only input for the decoder

    • If the encoder uses the LSTM cell, the output of the encoder would be the last return state and the last memory cell, i.e., \(h_t\) and \(c_t\)

  • Decoder

    • During the training stage, the decoder takes the previous return state \(h_{t-1}\) and the current \(Y_t\) as the input for the LSTM (concatenated). This is referred to as teacher forcing.

    • During the testing stage, the decoder would decode the output one at a time, taking the previous return state \(h_{t-1}\) and the previous return output \(Y_{t-1}\) as the inputs of the LSTM (concatenated). That is, no teacher-forcing during the testing stage.

Peeky Sequence-to-Sequence#

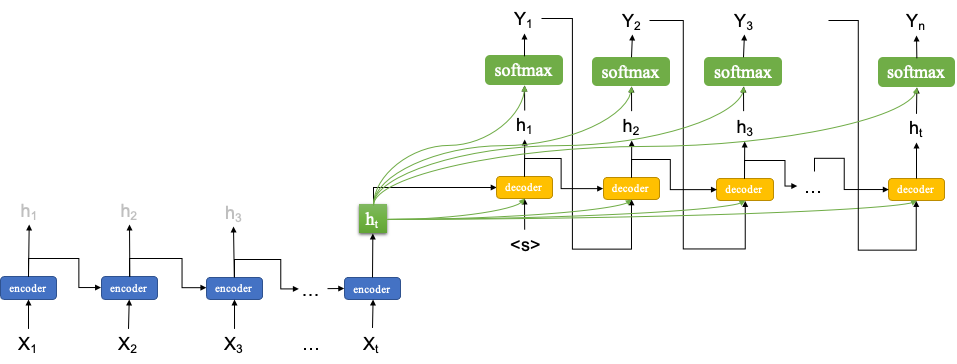
  • A variant of the seq-to-seq model, which makes available the last return state \(h_{t}\) from the encoder to every time step in the decoder.

  • An intuitive understanding of this peeky approach is that when decoding the contexts from the source input should be made available to all decoding steps.

Sequence-to-Sequence with Attention#

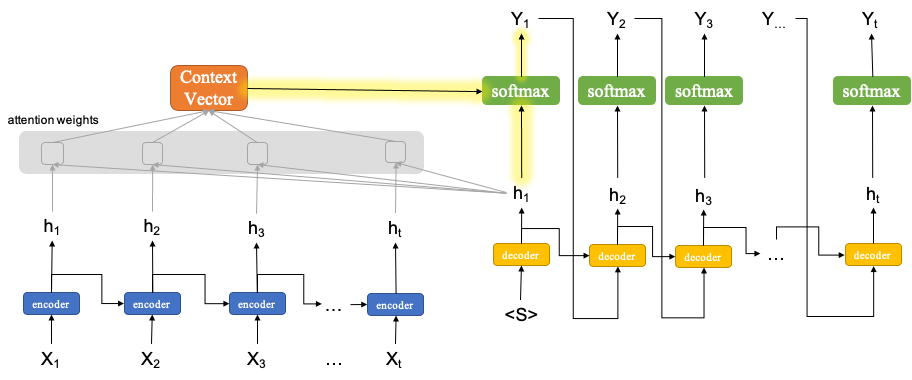
  • Attention mechansim can be seen as much more sophisticated design of the peeky approach.

  • The idea is that during the decoding stage, we need to consider the pairwise relationship (similarity) in-between the decoder state \(h_{t}\) and ALL the return states from the encoder.

  • An intuitive understanding is as follows. When decoding the translation of \(Y_{1}\), it is very likely that its translation is more relevant to some of the input words and less relevant to the others.

  • Therefore, the attention mechanism first needs to determine the relative pairwise relationship in-between the decoder \(h_{1}\) and all the encoder return states in order to get the attention weights.

  • There are many proposals regarding how to compute the attention weights. Please see a very nice review of Lilian Weng’s Attention? Attention!.

  • In the current Tensorflow implementation, there are three types of Attention layers:

  • With the attention weights, we can compute a context vector, which is like a weighted sum of the encoder return states.

  • We then use this weighted sum, along of the decoder return state \(h_{1}\), to compute the final output \(Y_{1}\).

  • This attention-mediated mechanism applies to every time step in the decoder.